Read - Implementation: Linked Lists
Topic 1 - Big O
A notation used to describe the efficiency/complexity of an algorithm or function. This efficiency is evaluated based on 2 factors:
- Running Time: the amount of time a function needs to be completed.
- Memory Space: the amount of memory resources a function uses to store data and instructions.
To analyze Time and Space, we should consider 4 key areas for analysis:
1 - Input Size
donated by ‘n’. The higher n is, the more likely there will be an increase to Time and Space.
Units of Measurement
For Running Time:
- The number of operations that are executed.
- The number of “Basic Operations” that are executed: the operation that is contributing the most to the total running time.
For Memory Space:
- The amount of space needed to hold the code for the algorithm.
- The amount of space needed to hold the input data.
- The amount of space needed for the output data.
- The amount of space needed to hold working space during the calculation.
Best Case, Worst Case, and Average Case
As industry standard, Big O describes the worst case for algorithm efficiency.
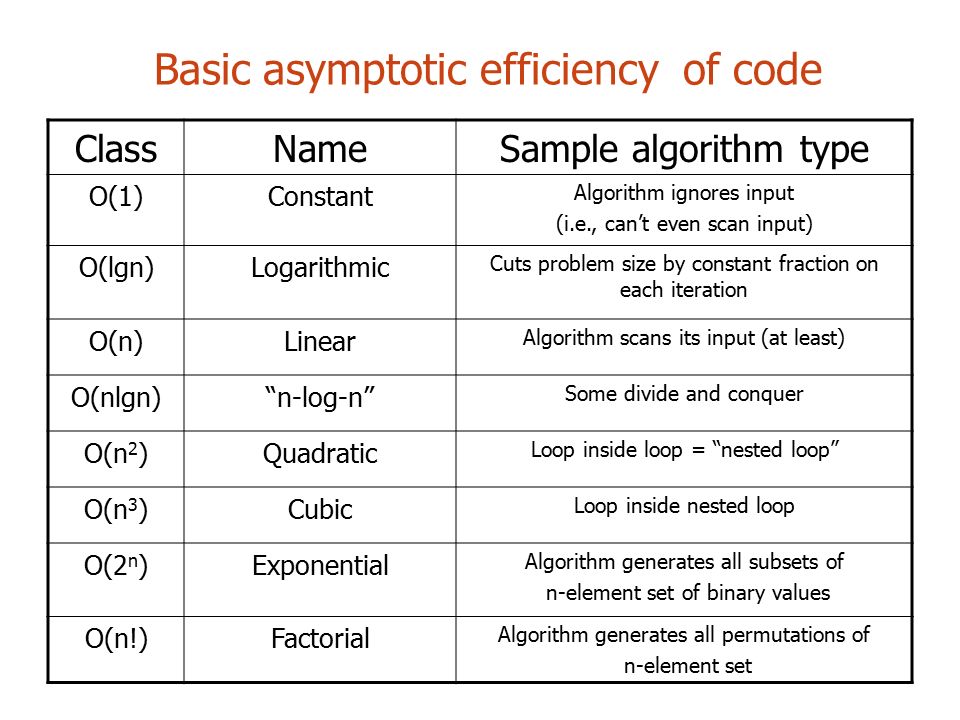
Orders of Growth
- Constant Complexity O(1) - complexity is independent of n. Example: a method that returns the sum of two numbers.
- Linear Complexity O(n) - complexity is directly dependent upon n. Example: a function with a loop.
- Logarithmic Complexity O(lgn) represents a function that sees a decrease in the rate of complexity growth, the greater our value of n. Example: binary search in arrays.
- Linearithmic Complexity O(nlgn) - complexity that grows with n, but also by lgn. Those functions grow faster than input size n, but not by much. Example: looping a binary search function.
- Quadratic Complexity O(n^2) - complexity that grows at a rate of input size n multiplied by n. Example: nested loops which perform iterative or recursive logic on all values of n.
- Cubic Complexity O(n^3) -a higher degree of what makes the quadratic complexity grow at such a high rate.
- Exponential Complexity O(2^n) - a very rapidly growing complexity, such that whatever our input size n, we are performing the same number of iterative or recursive loops as n.
- Factorial Complexity O(n!) - means that the our space and time requirements grow extremely fast, relative to our input size.
Topic 2 - Linked Lists
A Node is an item that lives in a linked list and contains data for the link.
A sequence of nodes that are connected to each other are known as a Linked List. In a linked list, each node references the next Node in the link. Linked lists are data structures.
Node properties:
- Next - this property contains the reference to the next node.
- Previous - this property contains the reference to the previous node.
- Head - a reference to the first node in a linked list.
- Current - a reference to the node that is currently being looked at.
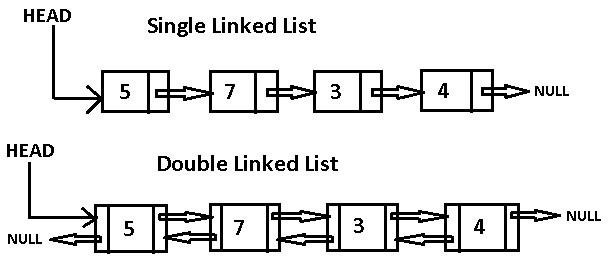
There are two types of linked list:
- Singly - has only one reference that points to the Next node in a linked list.
- Doubly - has two references that point to both the Next and Previous node.
Traversal
-
When traversing through a linked list, the Current variable tells us where exactly in the linked list we are and allows us to traverse (move) forward until we hit the end.
-
When traversing through a linked list, we depend on the Next value in each node to guide us where the next reference is pointing. Each node contains the Next property because what will lead us where the next node is and allow us to extract the data appropriately.
-
The best way to approach a traversal is using a
while()loop. This way, we will be continually checking if Next is not null. When Next reaches null, aNullReferenceExceptiongets thrown and our program will crash/end.
Adding a Node
Adding a node to the beginning of a linked list
We have to replace the current Head of the linked list with the new node, without losing the reference to the next node in the list. Steps:
- Create the new node and set the values of it by passing them as arguments into the
Add()method. - By default,
newNode.Nextis set to null. Set it to be the same to the location that the Head node is pointing towards. - Re-assign where Head is pointing too. The old head now will become is the new node is the new Head.
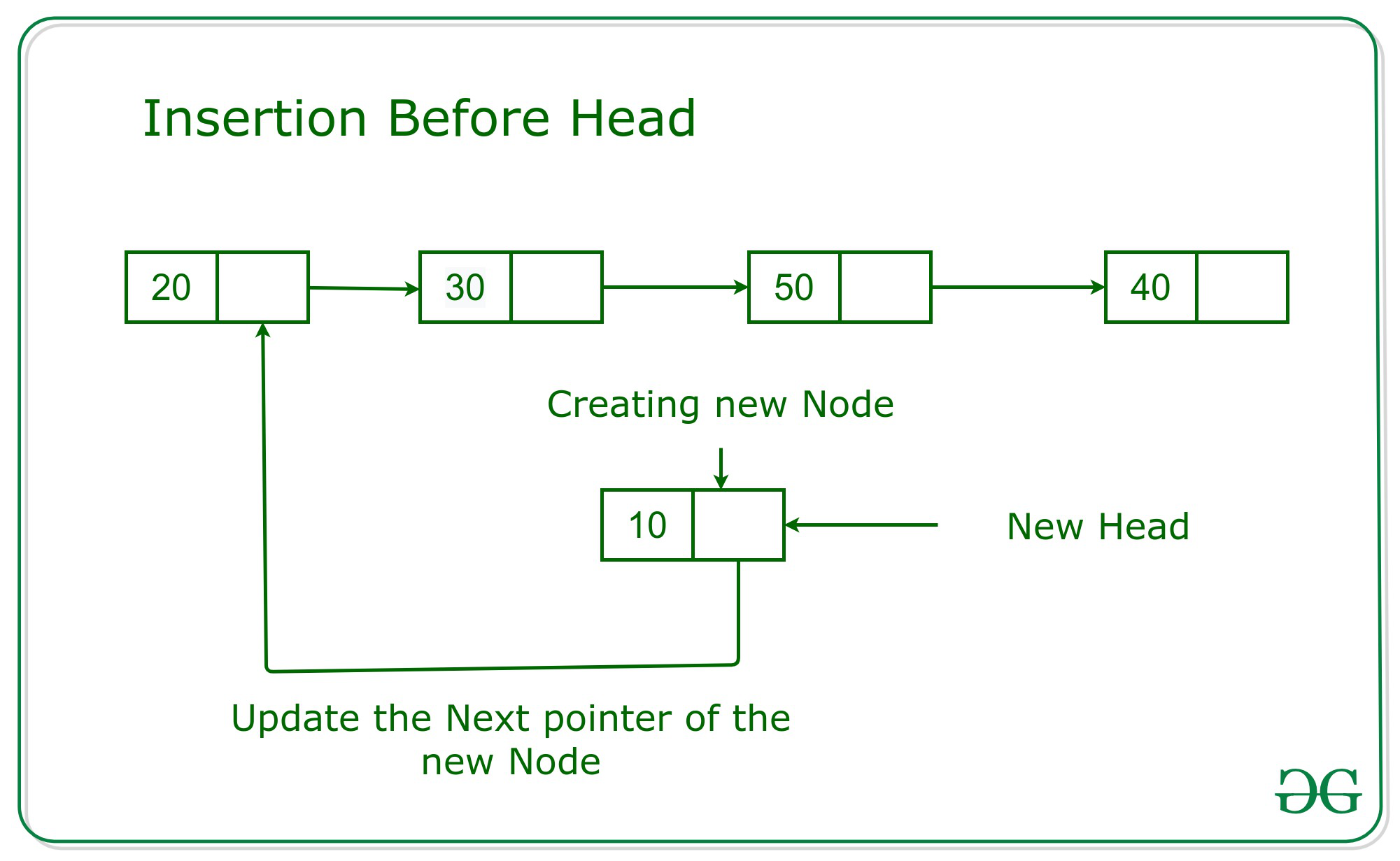
Big O will always be a O(1) for time and space complexity because it takes the same amount of time to add a new node to the beginning of the list, and no additional resources are being used.
Adding a node in the middle of a linked list
- Create the new node and set the values of it. The Next will be null because we haven’t yet attached it into the linked list.
- Either use an
AddBeforeorAddAftermethod to add the new node to the list. USing theAddBeforeapproach:- Transverse but before moving Current to the next node, check if the value of the next node is equal to the value of the existing node we are inserting before.
- Set the new node Next property to be the value of the existing node we are inserting before.
- Adjust current node Next to point to the newly created node.
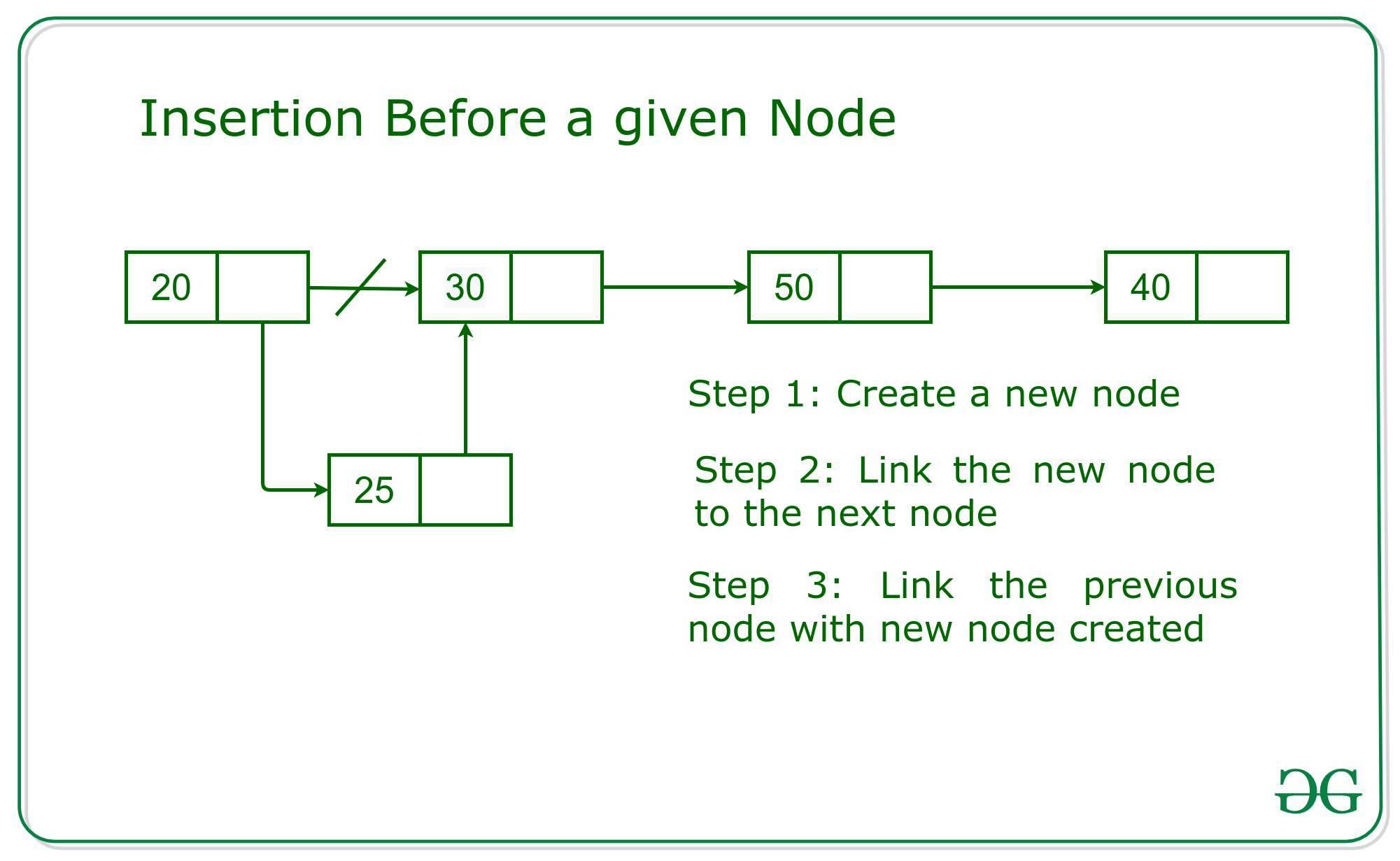
Big O will always be a O(n) for time and O(1) for space.
Print Out Nodes
Using the Current node and a while loop to traverse through the existing linked list.